873. Палиндромы
Непустая строка,
содержащая некоторое слово, называется палиндромом,
если это слово одинаково читается как слева направо, так и справа налево.
Имеется слово s, состоящее из n прописных букв латинского алфавита. Вычёркиванием из этого слова
некоторого набора символов можно получить палиндром. Найти количество способов
вычёркивания из данного слова некоторого (возможно, пустого) набора символов
таких, что полученная в результате строка являлась палиндромом. Способы,
различающиеся порядком вычёркивания символов, считаются одинаковыми.
Вход. Одно слово s длины n (1 ≤ n ≤ 60).
Выход. Вывести
одно целое число – количество способов вычёркивания.
|
Пример входа |
Пример выхода |
|
BAOBAB |
22 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Пусть dp[i][j]
хранит количество палиндромов, которое можно получить из подстроки si…sj удалением букв. Тогда dp[i][i] = 1, так как слово
из одного символа является палиндромом.
Пусть si = sj = X, подстрока si…sj имеет вид XPX. Здесь через P обозначена подстрока
si+1…sj-1. Разобьем палиндромы строки XPX на непересекающиеся
группы:
·
включающие левый символ X и не включающие правый
символ X. Их число равно количеству палиндромов в строке XP минус количество
палиндромов в P, то есть dp[i][j
– 1] – dp[i + 1][j – 1];

·
включающие правый символ X и не включающие левый
символ X. Их число равно количеству палиндромов в строке PX минус количество
палиндромов в P, то есть dp[i + 1][j] – dp[i + 1][j – 1];
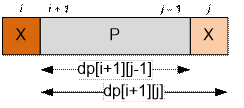
·
палиндромы строки P. Их количество равно dp[i
+ 1][j – 1]. Однако с каждым
палиндромом Q строки P мы можем
построить и палиндром XQX. То
есть палиндромов типа XQX также будет dp[i + 1][j – 1].

·
палиндром XX (один палиндром).
![]()
Общее количество палиндромов для случая si = sj равно
(dp[i][j – 1] – dp[i + 1][j – 1]) +
(dp[i
+ 1][j] – dp[i + 1][j – 1]) +
2 * dp[i
+ 1][j – 1] +
1
= dp[i][j – 1] + dp[i + 1][j] + 1.
Пусть si ≠ sj, подстрока si…sj имеет вид XPY (si = X, sj = Y). Разобьем палиндромы строки XPY на непересекающиеся группы:
·
включающие символ X и не включающие символ Y. Их
число равно количеству палиндромов в строке XP минус количество палиндромов в
P, то есть dp[i][j
– 1] – dp[i + 1][j – 1];

·
включающие символ Y и не включающие символ X. Их
число равно количеству палиндромов в строке PY минус количество палиндромов в
P, то есть dp[i + 1][j] – dp[i + 1][j – 1];
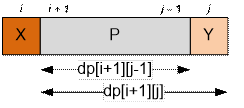
·
палиндромы строки P. Их количество равно dp[i
+ 1][j – 1].

Общее количество палиндромов для случая si ≠ sj равно
(dp[i][j – 1] – dp[i + 1][j – 1]) +
(dp[i
+ 1][j] – dp[i + 1][j – 1]) +
dp[i
+ 1][j – 1]
= dp[i][j
– 1] + dp[i + 1][j] – dp[i + 1][j – 1].
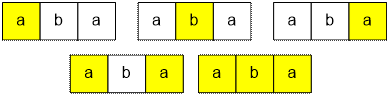
Пример
Из строки aba удалением
букв можно получить 5 палиндромов.
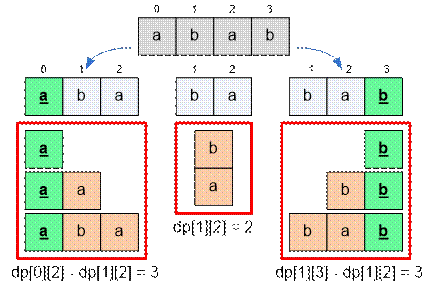
Рассмотрим строку abab = s0s1s2s3. Поскольку s0 ≠ s3, то подстрока s0…s3 имеет вид XPY. Отсюда dp[0][3]
=
(dp[0][2] – dp[1][2]) +
(dp[1][3] –
dp[1][2]) +
dp[1][2] =
= dp[0][2] + dp[1][3] – dp[1][2] = 5 + 5 – 2 = 8.
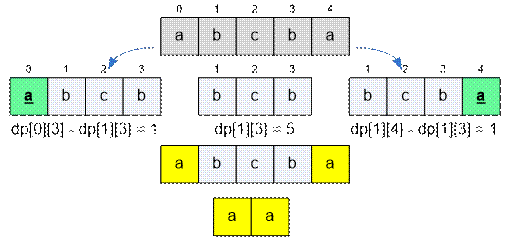
Рассмотрим строку abcba = s0s1s2s3s4. Поскольку s0 = s4, то подстрока s0…s4 имеет вид XPX. Отсюда dp[0][4]
=
(dp[0][3] – dp[1][3]) +
(dp[1][4] –
dp[1][3]) +
2 * dp[1][3] +
1 =
= dp[0][3] + dp[1][4] + 1 = 6 + 6 + 1 = 13.
Реализация алгоритма
В массиве s храним входную строку. Объявим массив dp.
#define MAX 65
char
s[MAX];
long long dp[MAX][MAX];
Читаем входную строку. Заполняем dp[i][i] = 1.
gets(s);
n = strlen(s);
memset(dp,0,sizeof(dp));
for(i
= 0; i < n; i++) dp[i][i] = 1;
Перебираем длины подстрок len и позиции их начала i.
for(len
= 1; len < n; len++)
for(i
= 0; i + len < n; i++)
{
j = i + len;
Для каждой такой подстроки si…sj
вычисляем значение dp[i][j] – количество палиндромов, которое
можно получить из нее удалением символов. Поскольку подстроки si…sj перебираются в порядке возрастания их длин, то
значения dp на всех подотрезках меньшей длины уже вычислены.
if (s[i] == s[j])
dp[i][j] = dp[i+1][j] + dp[i][j-1] + 1;
else
dp[i][j] = dp[i+1][j] + dp[i][j-1] -
dp[i+1][j-1];
}
Выводим ответ.
printf("%lld\n",dp[0][n-1]);
Реализация алгоритма – рекурсия
#include <stdio.h>
#include <string.h>
#define MAX 61
В массиве s храним входную строку. Объявим массив
dp.
char s[MAX];
long long dp[MAX][MAX];
int i, j,
len, n;
long long f(int i, int j)
{
Если i > j, то палиндромов не существует.
if (i > j) return 0;
Слово из
одного символа является палиндромом, установим dp[i][i] = 1.
if (i == j) return dp[i][j] = 1;
Если значение dp[i][j] уже вычислено, то
возвращаем его.
if (dp[i][j] != -1) return dp[i][j];
Вычисляем значение dp[i][j] в зависимости от того, одинаковы или не одинаковы
символы si и sj.
if (s[i] == s[j])
dp[i][j] = f(i + 1, j) + f(i, j - 1) + 1;
else
dp[i][j] = f(i + 1, j) + f(i, j - 1) - f(i + 1, j - 1);
return dp[i][j];
}
int main(void)
{
Основная часть программы. Читаем входную строку s. Инициализируем массив dp.
gets(s); n =
strlen(s);
memset(dp, -1, sizeof(dp));
Выводим ответ.
printf("%lld\n", f(0, n - 1));
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static String s;
static long dp[][];
static long f(int i, int j)
{
if (i > j) return 0;
if (i == j) return dp[i][j] = 1;
if (dp[i][j] != -1) return dp[i][j];
if (s.charAt(i) == s.charAt(j))
dp[i][j] = f(i + 1,j) + f(i,j - 1) + 1;
else
dp[i][j] = f(i + 1,j) + f(i,j - 1) - f(i + 1,j - 1);
return dp[i][j];
}
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
s = con.nextLine();
int n = s.length();
dp = new long[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
dp[i][j] = -1;
System.out.println(f(0,n-1));
con.close();
}
}